Nächste Seite: Berechnung aus der Geometrie Aufwärts: Trägheitseinfluß Vorherige Seite: Trägheitseinfluß Inhalt Index
Die Bestimmung des Massenträgheitsmoment aus der Pendelzeit mit dem Ansatz als physikalisches Pendel erlaubt eine zerstörungsfreie Messung. Der Dynamo muß dabei nicht zerlegt werden. Beim lightSPIN ist dies aufgrund der Leichtgängigkeit durch berührungslose Dichtungen und Kugellager möglich.
An dem Rotor (Massenträgheitsmoment ![]() , Masse
, Masse ![]() ) wird ein
physikalisches Pendel bzw. Körperpendel (
) wird ein
physikalisches Pendel bzw. Körperpendel (![]() ,
, ![]() ) befestigt (vgl. Bild
I.1).
) befestigt (vgl. Bild
I.1).
Sowohl bei einer Anfangsauslenkung von 20 wie 30![]() beträgt die
gemessene Periodenzeit (
beträgt die
gemessene Periodenzeit (![]() ) ca. 0,78s (über 10 bzw. 17 Schwingungen
gemittelt). Das Pendel ist ein 4mm dicker Holzstab (
) ca. 0,78s (über 10 bzw. 17 Schwingungen
gemittelt). Das Pendel ist ein 4mm dicker Holzstab (
![]() 0,66...0,67kg/dm
0,66...0,67kg/dm![]() ) mit der Masse
) mit der Masse ![]() . Das Loch an
einem Ende wird über die Masse
. Das Loch an
einem Ende wird über die Masse ![]() berücksichtigt; mit diesem Loch wird
der Holzstab auf dem Reibrad montiert. Das Massenträgheitsmoment
berücksichtigt; mit diesem Loch wird
der Holzstab auf dem Reibrad montiert. Das Massenträgheitsmoment ![]() und
der Abstand des Flächenschwerpunkt von der Rotationsachse
und
der Abstand des Flächenschwerpunkt von der Rotationsachse ![]() des Stabes
berechnet sich als:
des Stabes
berechnet sich als:
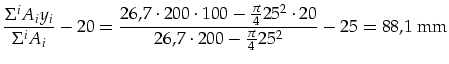 |
(I.1) | ||
| (I.2) | |||
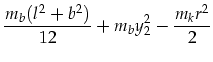 |
(I.3) | ||
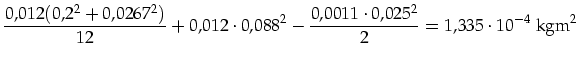 |
Mit der Gleichung (I.7) für die Schwingungsdauer ![]() eines
physikalischen Pendels bei kleinen Ausschlägen ergibt sich das
Massenträgheitsmoment des Rotors:
eines
physikalischen Pendels bei kleinen Ausschlägen ergibt sich das
Massenträgheitsmoment des Rotors:
Olaf Schultz, Hamburg-Harburg